The Art of Interface

Article 13

ECG processing — R-peaks detection

Category. Medical digital signal processing (DSP) software development.

Abstract. ECG R-peaks detection algorithm development — MatLab prototype of processing pipeline. Case contains algorithm description, full MatLab source code and ECG sample data files.

Librow Calculator Pro

Limited offer

Professional Librow Calculatorvisit

for free

  • Bessel functions
  • gamma function
  • complex numbers
Download
7.4 MB for Windows
Download MatLab ECG processing code (zip, 74 kB)

ECG processing

1. Introduction

The basic task of electrocardiogram — ECG — processing is R-peaks detection. There are some difficulties one can encounter in processing ECG: irregular distance between peaks, irregular peak form, presence of low-frequency component in ECG due to patient breathing etc. To solve the task the processing pipeline should contain particular stages to reduce influence of those factors. Present sample demonstrates such a pipeline. The aim is to show results of processing in main pipeline stages.

2. MatLab demonstration package

The demo package includes 5 files — two MatLab scripts, two data samples and description:

  • ecgdemo.m — main MatLab script,
  • ecgdemowinmax.m — window peak filter script,
  • ecgdemodata1.mat — first sample ECG data file,
  • ecgdemodata2.mat — second sample ECG data file,
  • readme.txt — description.

Some technical notes on demo:

  • To run the sample MatLab should be installed on your computer.
  • Unpack the sample and copy .m and .mat files into MatLab work directory.
  • Start up MatLab and type in:

    >> ecgdemo

3. How it works

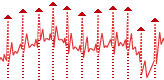
Let us have some digital ECG signal — that is our input data (fig. 1):

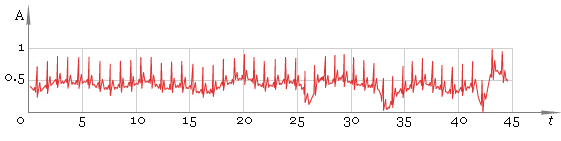Fig. 1. Original ECG. Fig. 1. Original ECG.

As one can see the ECG is uneven. Thus our first step is to straighten it. To say that in mathematical language, we should remove low-frequency component. The idea is to apply direct fast Fourier transform — FFT, remove low frequencies and restore ECG with the help of inverse FFT. Here is the result of FFT processing — fig. 2.

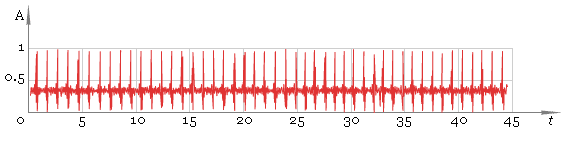Fig. 2. FFT filtered ECG. Fig. 2. FFT filtered ECG.

Our second step is to find local maxima. To do that we use windowed filter that “sees” only maximum in his window and ignores all other values. At this step we use window of default size. As result we get fig. 3.

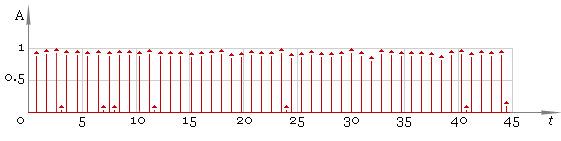Fig. 3. Filtered ECG - first pass. Fig. 3. Filtered ECG — first pass.

Now we should remove small values and preserve significant ones — fig. 4. Here we are using a threshold filter.

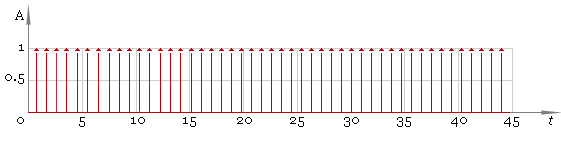Fig. 4. Peaks. Fig. 4. Peaks.

In this case the result is good but in general case we cannot be sure we have all the peaks. So the next step is to adjust filter window size and repeat filtering — fig. 5. Compare the result with fig. 3 — now filtering quality is much better.

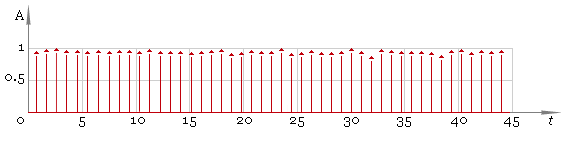Fig. 5. Filtered ECG - second pass. Fig. 5. Filtered ECG — second pass.

Now we are ready to get the final result and here it is: fig. 6.

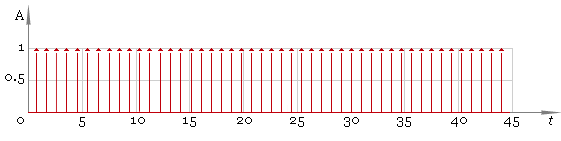Fig. 6. Peaks - final result. Fig. 6. Peaks — final result.
 
Write to the author of the article — Sergey Chernenko