The Art of Interface

Article 7

Alpha-trimmed mean filter

Category. Digital signal and image processing (DSP and DIP) software development.

Abstract. The article is a practical tutorial for alpha-trimmed mean filter understanding and implementation. Article contains theory, C++ source code, programming instructions and sample applications.

Librow Calculator Pro

Limited offer

Professional Librow Calculatorvisit

for free

  • Bessel functions
  • gamma function
  • complex numbers
Download
7.4 MB for Windows
Download alpha-trimmed mean filter for Win32 (zip, 603 kB)
Download alpha-trimmed mean filter C++ source code (zip, 2 kB)

Corrupted and restored images

1. Introduction to alpha-trimmed mean filter

Alpha-trimmed mean filter is windowed filter of nonlinear class, by its nature is hybrid of the mean and median filters. The basic idea behind filter is for any element of the signal (image) look at its neighborhood, discard the most atypical elements and calculate mean value using the rest of them. Alpha you can see in the name of the filter is indeed parameter responsible for the number of trimmed elements.

To get acquainted with filter window idea in signal and image processing read our “Filter window, or filter mask” article.

2. Understanding alpha-trimmed mean filter

Now let us see, how to get alpha-trimmed mean value in practice. The basic idea here is to order elements, discard elements at the beginning and at the end of the got ordered set and then calculate average value using the rest. For instance, let us calculate alpha-trimmed mean for the case, depicted in fig. 1.

Fig. 1. Alpha-trimmed mean calculation. Fig. 1. Alpha-trimmed mean calculation.

Thus, to get an alpha-trimmed mean we are to order elements, eliminate elements at the beginning and at the end of the got sequenced collection and get average of the remaining elements. That is all — now alpha-trimmed mean calculated and signal, 1D in our case, filtered by alpha-trimmed mean filter! Let us make resume and write down step-by-step instructions for processing by alpha-trimmed mean filter.

Alpha-trimmed mean filter algorithm:

  1. Place a window over element;
  2. Pick up elements;
  3. Order elements;
  4. Discard elements at the beginning and at the end of the got ordered set;
  5. Take an average — sum up the remaining elements and divide the sum by their number.

A couple of words about alpha parameter responsible for trimmed elements. In practice alpha is the number of elements to be discarded, for instance, in our case alpha is two. Since our filter is symmetric one alpha is an even nonnegative number less than size of the filter window. Minimum value for alpha parameter is zero and in this case alpha-trimmed mean filter degenerates into mean filter. Maximum value for alpha is filter window size minus one and in this case filter degenerates into median filter.

Now, when we have the algorithm, it is time to write some code — let us come down to programming.

3. 1D alpha-trimmed mean filter programming

In this section we develop 1D alpha-trimmed mean filter with window of size 5. Let us have 1D signal of length N as input. The first step is window placing — we do that by changing index of the leading element:

//   Move window through all elements of the signal
for (int i = 2; i < N - 2; ++i)

Pay attention, that we are starting with the third element and finishing with the last but two. The problem is we cannot start with the first element, because in this case the left part of the filter window is empty. We will discuss below, how to solve that problem.

The second step is picking up elements around, ok:

//   Pick up window elements
for (int j = 0; j < 5; ++j)
   window[j] = signal[i - 2 + j];

The third step is putting window elements in order. But we will use a code optimization trick here. As soon as we need only middle part of the ordered set we can omit putting in order last α/2 elements. So, it is enough to process just 5−α/2 elements:

//   End of the trimmed ordered set
const int end = 5 - (alpha >> 1);

Now:

//   Order elements (only necessary part of them)
for (int j = 0; j < end; ++j)
{
   //   Find position of minimum element
   int min = j;
   for (int k = j + 1; k < 5; ++k)
      if (window[k] < window[min])
         min = k;
   //   Put found minimum element in its place
   const element temp = window[j];
   window[j] = window[min];
   window[min] = temp;
}

To discard elements at the beginning of the ordered set let us define the proper constant:

//   Start of the trimmed ordered set
const int start = alpha >> 1;

The final step — taking the average:

//   Get result - the mean value of the elements in trimmed set
result[i - 2] = window[start];
for (int j = start + 1; j < end; ++j)
   result[i - 2] += window[j];
result[i - 2] /= N - alpha;

At last, let us write down the entire algorithm as function:

//   1D ALPHA-TRIMMED MEAN FILTER implementation
//     signal - input signal
//     result - output signal
//     N      - length of the signal
//     alpha  - filter alpha parameter
void _alphatrimmedmeanfilter(const element* signal, element* result,
   int N, int alpha)
{
   //   Start of the trimmed ordered set
   const int start = alpha >> 1;
   //   End of the trimmed ordered set
   const int end = 5 - (alpha >> 1);
   //   Move window through all elements of the signal
   for (int i = 2; i < N - 2; ++i)
   {
      //   Pick up window elements
      element window[5];
      for (int j = 0; j < 5; ++j)
         window[j] = signal[i - 2 + j];
      //   Order elements (only necessary part of them)
      for (int j = 0; j < end; ++j)
      {
         //   Find position of minimum element
         int min = j;
         for (int k = j + 1; k < 5; ++k)
            if (window[k] < window[min])
               min = k;
         //   Put found minimum element in its place
         const element temp = window[j];
         window[j] = window[min];
         window[min] = temp;
      }
      //   Get result - the mean value of the elements in trimmed set
      result[i - 2] = window[start];
      for (int j = start + 1; j < end; ++j)
         result[i - 2] += window[j];
      result[i - 2] /= 5 - alpha;
   }
}

Type element could be defined as:

typedef double element;

4. Treating edges

For all window filters there is some problem. That is edge treating. If you place window over first (last) element, the left (right) part of the window will be empty. To fill the gap, signal should be extended. For alpha-trimmed mean filter there is good idea to extend signal symmetrically, like this:

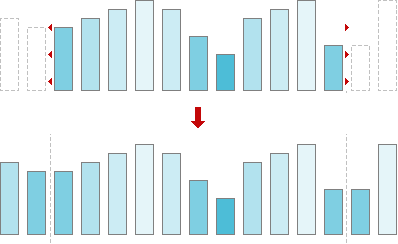Fig. 2. Signal extension. Fig. 2. Signal extension.

So, before passing signal to our alpha-trimmed mean filter function the signal should be extended. Let us write down the wrapper, that makes all preparations.

//   1D ALPHA-TRIMMED MEAN FILTER wrapper
//     signal - input signal
//     result - output signal
//     N      - length of the signal
//     alpha  - filter alpha parameter
void alphatrimmedmeanfilter(element* signal, element* result, int N, int alpha)
{
   //   Check arguments
   if (!signal || N < 1 || alpha < 0 || 4 < alpha || alpha & 1)
      return;
   //   Treat special case N = 1
   if (N == 1)
   {
      if (result)
         result[0] = signal[0];
      return;
   }
   //   Allocate memory for signal extension
   element* extension = new element[N + 4];
   //   Check memory allocation
   if (!extension)
      return;
   //   Create signal extension
   memcpy(extension + 2, signal, N * sizeof(element));
   for (int i = 0; i < 2; ++i)
   {
      extension[i] = signal[1 - i];
      extension[N + 2 + i] = signal[N - 1 - i];
   }
   //   Call alpha-trimmed mean filter implementation
   _alphatrimmedmeanfilter(extension + 2, result ? result : signal,
      N + 4, alpha);
   //   Free memory
   delete[] extension;
}

As you can see, our code takes into account some practical issues. First of all we check our input parameters — signal should not be NULL, signal length should be positive, alpha parameter should be even nonnegative number less than window size:

//   Check arguments
if (!signal || N < 1 || alpha < 0 || 4 < alpha || alpha & 1)
   return;

Second step — we check case N=1. This case is special one, because to build extension we need at least two elements. For the signal of 1 element length the result is the signal itself. As well pay attention, our alpha-trimmed mean filter works in-place, if output parameter result is NULL.

//   Treat special case N = 1
if (N == 1)
{
   if (result)
      result[0] = signal[0];
   return;
}

Now let us allocate memory for signal extension.

//   Allocate memory for signal extension
element* extension = new element[N + 4];

And check memory allocation.

//   Check memory allocation
if (!extension)
   return;

Now we are building extension.

//   Create signal extension
memcpy(extension + 2, signal, N * sizeof(element));
for (int i = 0; i < 2; ++i)
{
   extension[i] = signal[1 - i];
   extension[N + 2 + i] = signal[N - 1 - i];
}

Finally, everything is ready — filtering!

//   Call alpha-trimmed mean filter implementation
_alphatrimmedmeanfilter(extension, result ? result : signal, N + 4, alpha);

And to complete the job — free memory.

//   Free memory
delete[] extension;

Since we are using memory management function from standard library, we should include its header.

#include <memory.h>

5. 2D alpha-trimmed mean filter programming

In 2D case we have 2D signal, or image. The idea is the same, just now alpha-trimmed mean filter has 2D window. Window influences only the elements selection. All the rest is the same: ordering elements, trimming the got set and calculating average of the remaining elements. So, let us have a look at 2D alpha-trimmed mean filter programming. For 2D case we choose window of 3×3 size.

//   2D ALPHA-TRIMMED MEAN FILTER implementation
//     image  - input image
//     result - output image
//     N      - width of the image
//     M      - height of the image
//     alpha  - filter alpha parameter
void _alphatrimmedmeanfilter(const element* image, element* result,
   int N, int M, int alpha)
{
   //   Start of the trimmed ordered set
   const int start = alpha >> 1;
   //   End of the trimmed ordered set
   const int end = 9 - (alpha >> 1);
   //   Move window through all elements of the image
   for (int m = 1; m < M - 1; ++m)
      for (int n = 1; n < N - 1; ++n)
      {
         //   Pick up window elements
         int k = 0;
         element window[9];
         for (int j = m - 1; j < m + 2; ++j)
            for (int i = n - 1; i < n + 2; ++i)
               window[k++] = image[j * N + i];
         //   Order elements (only necessary part of them)
         for (int j = 0; j < end; ++j)
         {
            //   Find position of minimum element
            int min = j;
            for (int l = j + 1; l < 9; ++l)
            if (window[l] < window[min])
               min = l;
            //   Put found minimum element in its place
            const element temp = window[j];
            window[j] = window[min];
            window[min] = temp;
         }
         //   Target index in result image
         const int target = (m - 1) * (N - 2) + n - 1;
         //   Get result - the mean value of the elements in trimmed set
         result[target] = window[start];
         for (int j = start + 1; j < end; ++j)
            result[target] += window[j];
         result[target] /= 9 - alpha;
      }
}

6. Treating edges in 2D case

As for 1D case in 2D case we should extend our input image as well. To do that we are to add lines at the top and at the bottom of the image and add columns to the left and to the right.

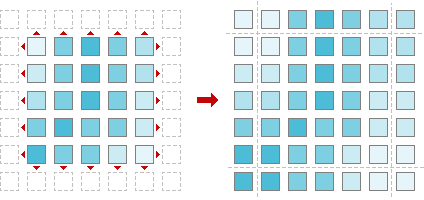Fig. 3. Image extension. Fig. 3. Image extension.

Here is our wrapper function, that does that job.

//   2D ALPHA-TRIMMED MEAN FILTER wrapper
//     image  - input image
//     result - output image
//     N      - width of the image
//     M      - height of the image
//     alpha  - filter alpha parameter
void alphatrimmedmeanfilter(element* image, element* result,
   int N, int M, int alpha)
{
   //   Check arguments
   if (!image || N < 1 || M < 1 || alpha < 0 || 8 < alpha || alpha & 1)
      return;
   //   Allocate memory for signal extension
   element* extension = new element[(N + 2) * (M + 2)];
   //   Check memory allocation
   if (!extension)
      return;
   //   Create image extension
   for (int i = 0; i < M; ++i)
   {
      memcpy(extension + (N + 2) * (i + 1) + 1,
         image + N * i,
         N * sizeof(element));
      extension[(N + 2) * (i + 1)] = image[N * i];
      extension[(N + 2) * (i + 2) - 1] = image[N * (i + 1) - 1];
   }
   //   Fill first line of image extension
   memcpy(extension, extension + N + 2, (N + 2) * sizeof(element));
   //   Fill last line of image extension
   memcpy(extension + (N + 2) * (M + 1),
      extension + (N + 2) * M,
      (N + 2) * sizeof(element));
   //   Call alpha-trimmed mean filter implementation
   _alphatrimmedmeanfilter(extension, result ? result : image,
      N + 2, M + 2, alpha);
   //   Free memory
   delete[] extension;
}

7. Alpha-trimmed mean filter library

Now we have four functions, two of them are for processing 1D signals by alpha-trimmed mean filter, and other two are for filtering 2D images. It is time to put everything together and create small alpha-trimmed mean filter library. Let us write code for header file.

//   alphatrimmedmeanfilter.h - declarations for 
//   1D and 2D alpha-trimmed mean filter routines
//
//   The code is property of LIBROW
//   You can use it on your own
//   When utilizing credit LIBROW site

#ifndef _ALPHATRIMMEDMEANFILTER_H_
#define _ALPHATRIMMEDMEANFILTER_H_

//   Signal/image element type
typedef double element;

//   1D ALPHA-TRIMMED MEAN FILTER, window size 5
//     signal - input signal
//     result - output signal, NULL for inplace processing
//     N      - length of the signal
//     alpha  - filter alpha parameter
void alphatrimmedmeanfilter(element* signal, element* result,
   int N, int alpha);

//   2D ALPHA-TRIMMED MEAN FILTER, window size 3x3
//     image  - input image
//     result - output image, NULL for inplace processing
//     N      - width of the image
//     M      - height of the image
//     alpha  - filter alpha parameter
void alphatrimmedmeanfilter(element* image, element* result,
   int N, int M, int alpha);

#endif

Our library is ready. The code we have written is good both for Linux/Unix and Windows platforms. You can download full alpha-trimmed mean filter library source code here:

Download alpha-trimmed mean filter C++ source code (zip, 2 kB)

Full listings of library files are available online as well:

And now — a couple of applications to play around!

8. Alpha-trimmed mean filter: image restoration

Download alpha-trimmed mean filter for Win32 (zip, 603 kB)

We have created a couple of applications to show alpha-trimmed mean filter capabilities in restoration images corrupted by impulse noise. The demo package includes 4 files — two applications, sample image and description:

  • alphatrimmedmean.exe — alpha-trimmed mean filter,
  • corrupter.exe — impulse noise generator,
  • sample.bmp — 24-bit sample image,
  • readme.txt — description.

Be aware of the fact, that this sample uses OpenGL, so it should be supported by your system (usually that is the case).

9. Step 1: prepare corrupted image

We have created impulse noise generator that will help us to prepare corrupted image. Start up corrupter.exe application and load image to be corrupted. Choose Set >> Corruption... or click N button in toolbar and set noise level at 5–15%. Click OK. Then save corrupted image.

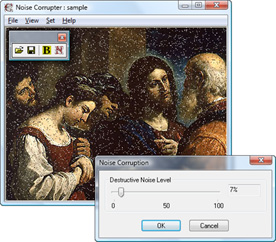Fig. 4. Corruption by impulse noise. Screenshot. Fig. 4. Corruption by impulse noise.

10. Step 2: restore corrupted image

Start up alphatrimmedmean.exe application. Load the saved corrupted image. Set alpha parameter to 6: Set >> Alpha... or click α-button in toolbar and select 6 in dialog's combo-box, click OK.

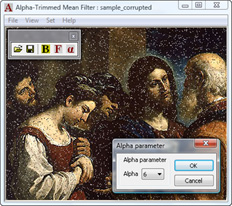Fig. 5. Alpha parameter selection. Screenshot. Fig. 5. Alpha parameter selection.

Apply alpha-trimmed mean filter by choosing Set >> Filter or clicking F-button in toolbar. See the result. If necessary, filter the image once more.

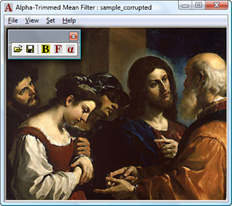Fig. 6. Image restored by alpha-trimmed mean filter. Screenshot. Fig. 6. Image restored by alpha-trimmed mean filter.
 
Write to the author of the article — Sergey Chernenko