The Art of Interface

Article 11 — Appendix A.22

log or lg — decimal logarithmic function

Category. Mathematics.

Abstract. Decimal logarithm: definition, plot, properties and identities.

Reference. This article is a part of Librow scientific formula calculator project.

Librow Calculator Pro

Limited offer

Professional Librow Calculatorvisit

for free

  • Bessel functions
  • gamma function
  • complex numbers
Download
7.4 MB for Windows

1. Definition

Decimal logarithmic function is the inverse of the 10-base exponential function

10x

2. Plot

Decimal logarithmic function is defined on positive part of the real axis — so, its domain is (0, +∞). 0 is singular point. Function plot is depicted below — fig. 1.

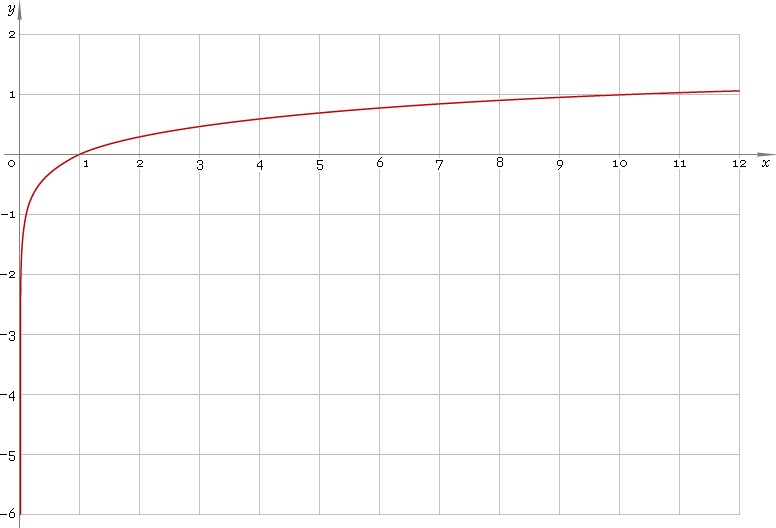Fig. 1. Plot of the decimal logarithmic function y = log x. Fig. 1. Plot of the decimal logarithmic function y = logx.

Function codomain is entire real axis.

3. Identities

By definition:

log10x ≡ x

Reciprocal argument:

log(1/x) = −logx

Product and ratio of arguments:

log(xy) = logx + logy
log(x /y) = logx − logy

Power of argument:

logxa = a logx

Base change:

logax = logx /loga
logax = logbx /logba

4. Support

Decimal logarithmic function log or lg of the real argument is supported by free version of the Librow calculator.

Decimal logarithmic function log or lg of the complex argument is supported by professional version of the Librow calculator.

5. How to use

To calculate decimal logarithm of the number:

log(2);

To calculate decimal logarithm of the current result:

log(rslt);

To calculate decimal logarithm of the number x in memory:

log(mem[x]);