The Art of Interface

Article 11 — Appendix A.25

sec — trigonometric secant function

Category. Mathematics.

Abstract. Trigonometric secant: definition, plot, properties, identities and table of values for some angles.

Reference. This article is a part of Librow scientific formula calculator project.

Librow Calculator Pro

Limited offer

Professional Librow Calculatorvisit

for free

  • Bessel functions
  • gamma function
  • complex numbers
Download
7.4 MB for Windows

1. Definition

Secant of the angle is ratio of the hypotenuse to adjacent leg.

2. Plot

Secant is 2π periodic function defined everywhere on real axis, except its singular points π/2 + πn, n=0, ±1, ±2, ... — so, function domain is (−π/2 + πn, π/2 + πn), n∈N. Its stalactite-stalagmite plot is depicted below — fig. 1.

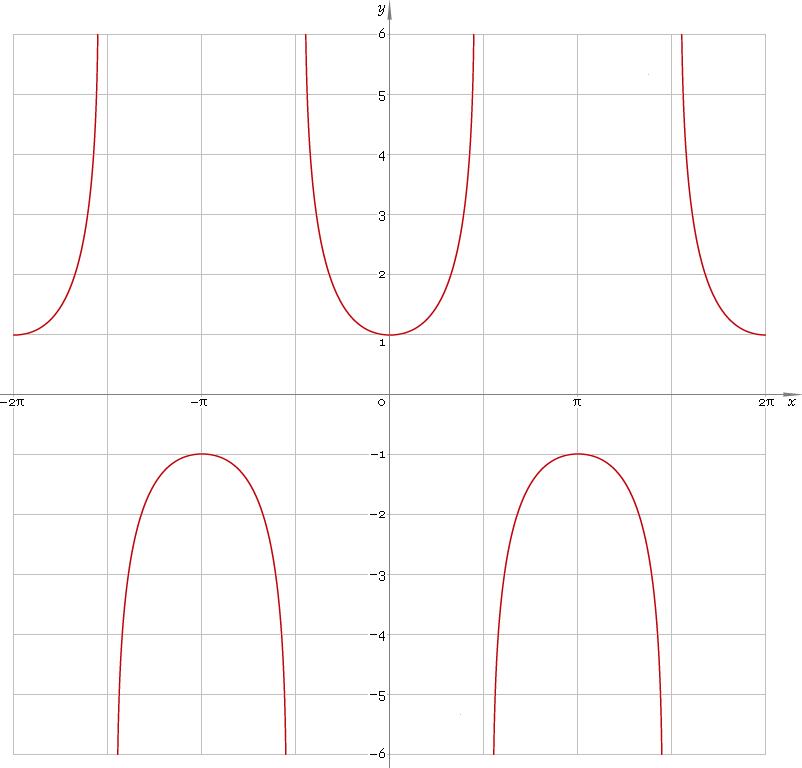Fig. 1. Plot of the secant function y = sec x. Fig. 1. Plot of the secant function y = secx.

Function codomain is entire real axis with gap in the middle: (−∞, −1]∪[1, +∞).

3. Identities

Base:

csc−2φ + sec−2φ = 1

and its consequences:

secφ = ±1 /√(1 − sin2φ)
secφ = ±√(1 + tan2φ)
secφ = ±√(1 + cot2φ) / cotφ
secφ = ±cscφ /√(csc2φ − 1)

By definition:

secφ ≡ 1 /cosφ

Properties — symmetry, periodicity, etc.:

sec−φ = cscφ
secφ = sec(φ + 2πn), where n = 0, ±1, ±2, ...
secφ = −sec(π − φ)
secφ = −sec(π + φ)
secφ = csc(π/2 + φ)

Sum of angles:

sec(φ + ψ + χ) = secφ secψ secχ / (1 − tanφ tanψ − tanφ tanχ − tanψ tanχ)

Some angles:

Angle φValue secφ
01
π/12√6 − √2
π/10√(50 − 10√5) /5
π/8√(2 − √2)
π/62√3 /3
π/5√5 − 1
π/4√2
3π/10√(50 + 10√5) /5
π/32
3π/8√(4 + 2√2)
2π/5√5 + 1
5π/12√6 + √2
Table 1. Secant for some angles.

4. Support

Trigonometric secant function sec of the real argument is supported by free version of the Librow calculator.

Trigonometric secant function sec of the complex argument is supported by professional version of the Librow calculator.

5. How to use

To calculate secant of the number:

sec(-1);

To calculate secant of the current result:

sec(rslt);

To calculate secant of the angle φ in memory:

sec(mem[φ]);