The Art of Interface

Article 11 — Appendix A.33

Γ or Gamma — gamma function

Category. Mathematics.

Abstract. Gamma function: definition, graph, properties and identities.

Reference. This article is a part of Librow professional formula calculator project.

See also. Special case of integer numbers — factorial n!.

Librow Calculator Pro

Limited offer

Professional Librow Calculatorvisit

for free

  • Bessel functions
  • gamma function
  • complex numbers
Download
7.4 MB for Windows

1. Definition

Gamma function is defined as integral

Gamma function definition

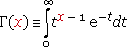
or

Gamma function definition

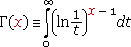
2. Plot

Gamma function defined everywhere on real axis, except its singular points n = 0, −1, −2, ... — so, function domain is ...∪(−2, −1)∪(−1, 0)∪(0, +∞). Its plot is depicted below — fig. 1.

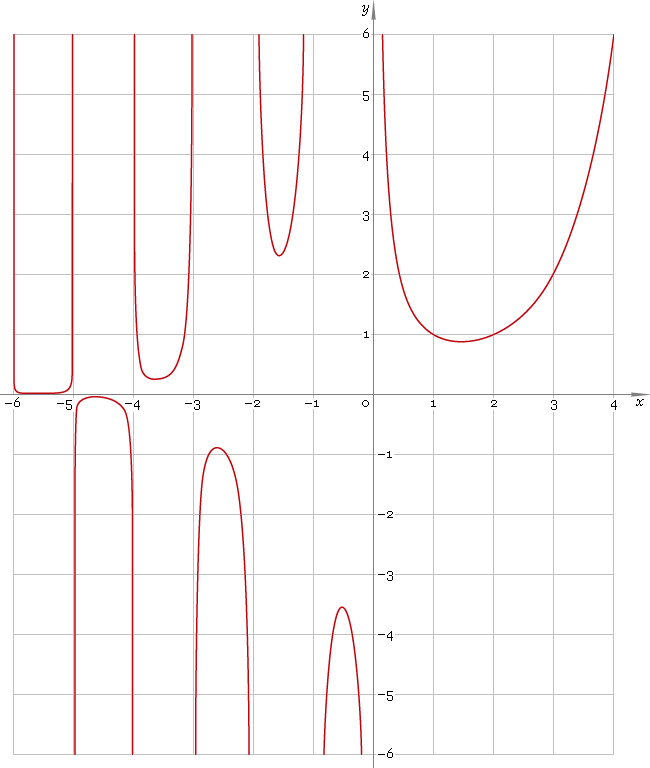Fig. 1. Plot of the gamma function y = Gamma(x). Fig. 1. Plot of the gamma function y = Γ(x).

Function codomain is entire real axis except 0: (−∞, 0)∪(0, +∞).

3. Identities

Connection to factorial:

Γ(n) = (n − 1)!

Factorial-like properties:

Γ(x + 1) = x Γ(x) Γ(1 − x) = −x Γ(−x)

Extension to negative half-axis:

Γ(1 − x) = π/[Γ(x) sin(πx)]

Doulbe argument:

Γ(2x) = (2π)−1/2 22x − 1/2 Γ(x) Γ(x + 1/2)

Triple argument:

Γ(3x) = (2π)−1 33x − 1/2 Γ(x) Γ(x + 1/3) Γ(x + 2/3)

Quadruple argument:

Γ(4x) = (2π)−3/2 44x − 1/2 Γ(x) Γ(x + 1/4) Γ(x + 1/2) Γ(x + 3/4)

Genaral formula for multiple argument:

Γ(nx) = (2π)(1−n)/2 nnx − 1/2 Γ(x) Γ(x + 1/n) ... Γ(x + (n − 1)/n)

Half-integer argument:

Γ(−5 /2) = −8 /15 √π
Γ(−3 /2) = 4 /3 √π
Γ(−1 /2) = −2 √π
Γ(1 /2) = √π
Γ(3 /2) = 1 /2 √π
Γ(5 /2) = 3 /4 √π

and in general:

Γ(1/2 + n) = (2n − 1)!! /2n√π = 1 × 3 × 5 × ... × (2n − 1) /2n√π

for negative values:

Γ(1/2 − n) = (−1)n2n/(2n − 1)!! √π = (−1)n2n/[1 × 3 × 5 × ... × (2n − 1)] √π

as well, for positive odd n:

Γ(n /2) = (n − 2)!! /2(n − 1)/2 √π

and for negative odd n:

Γ(n /2) = (−1)(n + 1)/2 2(n + 1)/2/n!! √π

4. Support

Gamma function Γ or Gamma of the complex argument is supported by professional version of the Librow calculator.

5. How to use

To calculate gamma function of the number:

Γ(-1.5);

or

Gamma(-1.5);

To calculate gamma function of the current result:

Γ(rslt);

or

Gamma(rslt);

To calculate gamma function of the number x in memory:

Γ(mem[x]);

or

Gamma(mem[x]);