The Art of Interface

Article 11 — Appendix A.38

ceil — ceiling function

Category. Mathematics.

Abstract. Ceiling: definition, plot and properties.

Reference. This article is a part of Librow professional formula calculator project.

See also. Floor function.

Librow Calculator Pro

Limited offer

Professional Librow Calculatorvisit

for free

  • Bessel functions
  • gamma function
  • complex numbers
Download
7.4 MB for Windows

1. Definition

Ceiling is the nearest integer to the righ — smallest integer greater than or equal to the argument.

2. Plot

Ceiling function defined everywhere on real axis — so, its domain is (−∞, +∞). Its stair-like plot is depicted below — fig. 1.

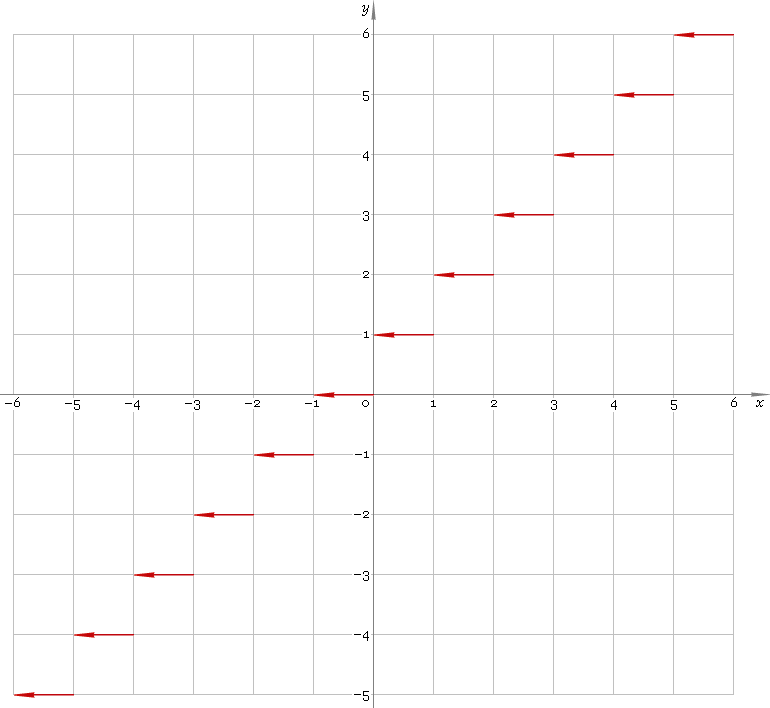Plot of the ceiling function y = ceil x. Fig. 1. Plot of the ceiling function y = ceilx.

Function codomain is the set of integer numbers.

3. Properties

When using the function be aware, that in general case:

ceil(x) + ceil(y) ≠ ceil(x + y)
ceil(x) − ceil(y) ≠ ceil(x − y)
ceil(x) ceil(y) ≠ ceil(x y)
ceil(x) /ceil(y) ≠ ceil(x /y)

4. Support

Ceiling function ceil of the complex argument is supported by professional version of the Librow calculator.

5. How to use

To calculate ceiling of the number:

ceil(-1.8);

To calculate ceiling of the current result:

ceil(rslt);

To calculate ceiling of the number x in memory:

ceil(mem[x]);