The Art of Interface

Article 11 — Appendix A.39

floor — floor function

Category. Mathematics.

Abstract. Floor: definition, plot and properties.

Reference. This article is a part of Librow professional formula calculator project.

See also. Ceiling function.

1. Definition

Floor is the nearest integer to the left — the larget integer less than or equal to the argument.

2. Plot

Floor function defined everywhere on real axis — so, its domain is (−∞, +∞). Its stair-like plot is depicted below — fig. 1.

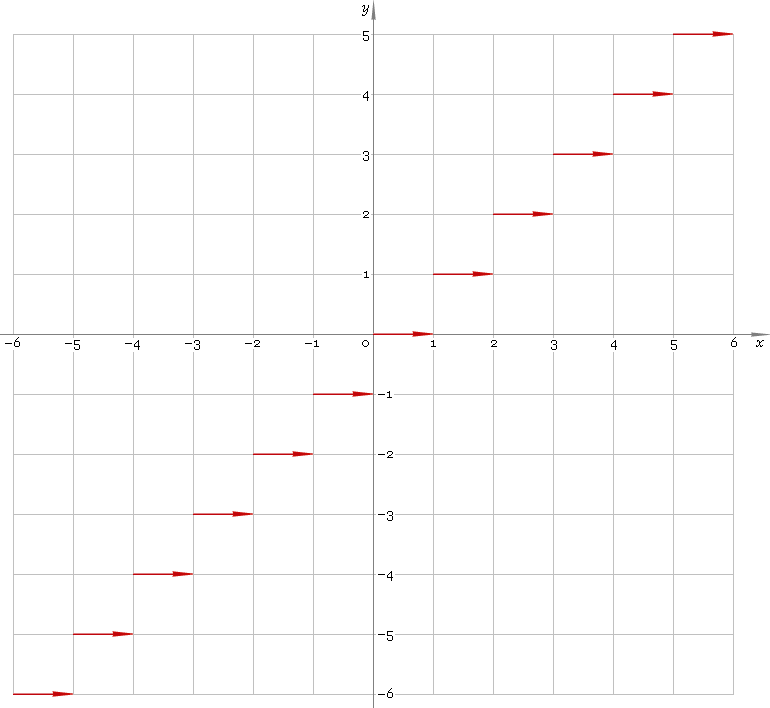Plot of the floor function y = floor x. Fig. 1. Plot of the floor function y = floorx.

Function codomain is the set of integer numbers.

3. Properties

When using the function be aware, that in general case:

floor(x) + floor(y) ≠ floor(x + y)
floor(x) − floor(y) ≠ floor(x − y)
floor(x) floor(y) ≠ floor(x y)
floor(x) /floor(y) ≠ floor(x /y)

4. Support

Floor function floor of the complex argument is supported by professional version of the Librow calculator.

5. How to use

To get floor of the number:

floor(-1.8);

To get floor of the current result:

floor(rslt);

To get floor of the number x in memory:

floor(mem[x]);