The Art of Interface

Article 11 — Appendix A.5

arcosh or arch — arc-hyperbolic cosine function

Category. Mathematics.

Abstract. Arc-hyperbolic cosine: definition, plot, properties and identities.

Reference. This article is a part of Librow scientific formula calculator project.

Librow Calculator Pro

Limited offer

Professional Librow Calculatorvisit

for free

  • Bessel functions
  • gamma function
  • complex numbers
Download
7.4 MB for Windows

1. Definition

Arc-hyperbolic cosine is inverse of hyperbolic cosine function. With the help of natural logarithm it can be represented as:

arcoshx ≡ ln[x + √(x2 − 1)]

2. Plot

Arc-hyperbolic cosine is monotone function defined in the range [1, +∞). Its plot is depicted below — fig. 1.

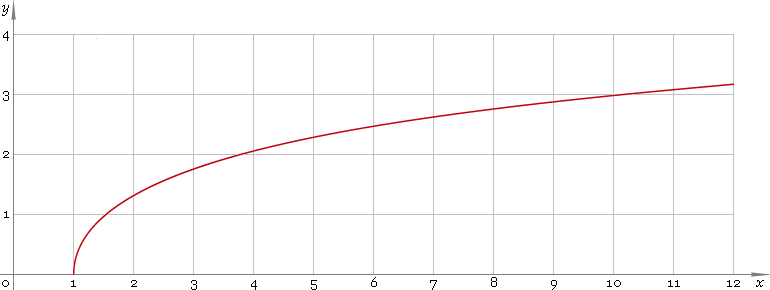Fig. 1. Plot of the arc-hyperbolic cosine function y = arcosh x. Fig. 1. Plot of the arc-hyperbolic cosine function y = arcoshx.

Function codomain is non-negative part of real axis: [0, +∞).

3. Identities

Reciprocal argument:

arcosh(1/x) = arsechx

Sum and difference:

arcoshx + arcoshy = arcosh{xy + √[(x2 − 1)(y2 − 1)]}
arcoshx − arcoshy = arcosh{xy − √[(x2 − 1)(y2 − 1)]}
arsinhx + arcoshy = arsinh{xy + √[(x2 + 1)(y2 − 1)]} = arcosh[y√(x2 + 1) + x√(y2 − 1)]

4. Support

Arc-hyperbolic cosine function arcosh or arch of the real argument is supported by free version of the Librow calculator.

Arc-hyperbolic cosine function arcosh or arch of the complex argument is supported by professional version of the Librow calculator.

5. How to use

To calculate arc-hyperbolic cosine of the number:

arcosh(2);

To calculate arc-hyperbolic cosine of the current result:

arcosh(rslt);

To calculate arc-hyperbolic cosine of the number x in memory:

arcosh(mem[x]);