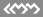| LIBROW | ® |
| Products | Solutions | Vehicles | Articles | Inquiry | Contacts | My account |
Article 20
Digital instrument cluster for Jeep Wrangler
Limited offer
Professional Librow Calculatorvisit
for free
- Bessel functions
- gamma function
- complex numbers
7.4 MB for Windows

1. Introduction
People driving Jeep Wrangler are special ones. They put second battery under hood, protect vehicle bottom with steel sheets and keep factory repair manual in the glove compartment for the case they stuck with their Jeep in wild out of mobile network reach. To those special ones dedicated.
2. Digital instrument cluster — housing
New digital dashboard is developed for Jeep Wrangler to substitute the original mechanical one — fig. 1.
 Fig. 1. Jeep Wrangler 2012 original instrument cluster.
Fig. 1. Jeep Wrangler 2012 original instrument cluster.
Call original dashboard mechanical is somewhat conditional in our case: it has gliders, which are mechanics, of course, but inside it is completely electronic. Even telltale bulbs are not bulbs indeed, but LEDs — light emitting diodes — soldered to the PCB — printed circuit board. That is the reason, by the way, in case some “bulb” is out the whole panel to be replaced (which is not that necessary if you know how to solder SMD components).
The major difficulty in development of substitution is new digital dashboard to be in compliance with existing dimensions of the installation compartment, so there is little space for varying cluster size and form. In its turn this fact puts serious restrictions on dimensions of LCD — liquid crystal display — one can put inside the digital instrumentation. For our project we have selected 260 mm × 96 mm TFT panel with 246 mm × 79 mm view area. Here is how this screen looks like — fig. 2.
 Fig. 2. Digital instrument cluster LCD.
Fig. 2. Digital instrument cluster LCD.
This very wide, unusually looking display is rugged automotive TFT of DVGA — double-VGA — format. As soon as we familiar with restrictions and have selected the screen, we can draw the housing assembly — fig. 3.
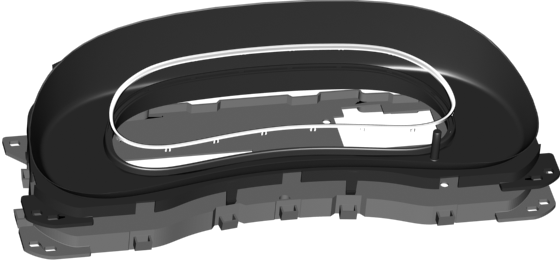 Fig. 3. Digital instrument cluster housing.
Fig. 3. Digital instrument cluster housing.
As its part the dashboard housing assembly has silver decorative frame to be in harmony with original dashboard style. Pay attention that original silver gauge frames are in harmony with silver inserts of the Jeep interior. So, the decoration is necessary to maintain interior style integrity.
3. Digital instrument cluster — graphical design
Now, when we have screen and its opening in housing, we can create a graphical design. Instrumentation set is traditional: temperature, fuel, RPM and speed gauges, counters, turn and state indicators — fig. 4.
 Fig. 4. Digital instrument cluster graphical design.
Fig. 4. Digital instrument cluster graphical design.
As soon as our cluster is virtual one, we are going to get advantage of its virtuality. For digital version of gauges we substitute gliders with segments, or arcs of dynamic color — something not possible for mechanical version. Segments can change their color from neutral yellow to red for critical values and green for eco range of RPM. Trip counters we will animate for smooth transition between values. State and turn indicators behavior we will soften with transparency animation.
4. Digital instrument cluster — programming
Real-time graphics rendering we are putting upon embedded graphics engine — EGE. Highly optimized rendering techniques of EGE make programming of the cluster a breeze. The video below shows programmed digital dashboard in action — video 1. Video 1. Digital instrument cluster for Jeep Wrangler — design.The outcome of the project is Jeep Wrangler 3D digital dashboard with the following characteristics:
| Digital instrument cluster characteristics | |
|---|---|
| Refresh rate | 60 Hz |
| Graphics format | RGB 16 bit |
| Buffering | Double |
| Resolution | 800×256 |
Here is the finally assembled digital instrument cluster in action — video 2.
Video 2. Digital instrument cluster for Jeep Wrangler.5. To learn more
Details on manufacturing of digital instrument clusters for cars and trucks:

|
Comprehensive service in graphical design for digital instrument clusters:
|

|
Full cycle of digital instrument cluster hardware development:
|

|
Full cycle of digital instrument cluster firmware development:
|

|
Full cycle of digital instrument cluster housing development:
|
|
|
|||||||||||||
|
|||||||||||||